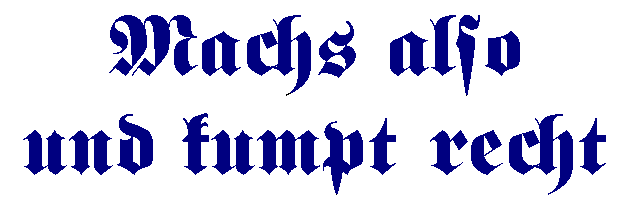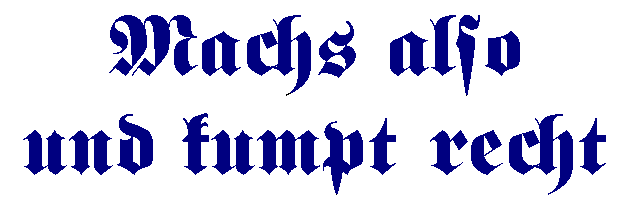Back to the Main Entrance
Teaching to understand - even Informatics!
by Klaus Kohl
Survey:
- A. IT Instruction today
- B. Demands to a modern technological instruction
- C. A possible way to an adequate understanding
- D. Outlook and end
Teaching to understand - even Informatics!!
by Klaus Kohl
A. IT instruction today
A 1. Situation
The computer is - maybe it's "only" the pocket calculator - in possession of the school. School owns it - or is it owning the school?
Informationstechnische Grundbildung - ITG / NIT - Neue Informationstechnologien - (as they are called in German) are penetrating all types of instruction, classroom-computers will enable an education no longer obstructed by frames of singular subjects or different classes. The World Wide Web Internet Data Highway at last will enable to come true the reality of an education no longer bothering the limits of schools, countries or continents. The goal of teaching Informatics is to learn about possibilities of the new technologies and also awareness to the dangers of their misuse. But scarcely it is intended to learn anything about the way the machines work or the programs running on them.
A 2. How did this come up?
Turning away from understanding the machine seems to be essential when you realize its complexity - still marching on to a higher grade: A modern processor - the central processing unit - contains [1] about 5 millions of transistor elements on its chip. I refer to the "Pentium" - do you remember the gloating complacent rumor in the media, when the possibility of a malfunction had turned out? A comparison: A month counts about 2.5 million seconds. Now imagine a genious expert of electronics, detecting by only one second the function and purpose of a transistor and the right position of it. This Superman (or Supergirl) would need two months of uninterrupted work (without eating or sleeping) to read the concept of the wiring diagram... You see: No human beeing would be able to understand a ready-made computer by all its details! Even more will that conclusion fit to the programs. Here are not millions but umpteens of millions steps 'normal'. Do you really believe Bill Gates knows all about Windows? - Why should we in school delay with the details of the computer and its programs?
We should use it and be glad and thankful to a mankind being able to create such huge works as pyramids and cathedrals (and computers anyway)!
A 3. And what should be wrong with that?
Maybe it isn't false at all, but I think that to be a mistake, maybe I have some supporters. I refer to two texts, the first one dealing specially with the computer:
Ernst Schuberth: Erziehung in einer Computergesellschaft, (Education within the Computerized Society) Verlag Freies Geistesleben, Stuttgart 1990, p. 294 f.:
"It is a demand (by Rudolf Steiner) that all instruction must refer to the conditions of human life. This is valid especially to data engineering. This must not result as negative. At most it should be considered negative that man looks at the machine to be a metaphor of himself and to compare his thinking to data processing by a machine - however a widespread idea. These impasses of cognition do not deal directly with what the technology is and what it is not. Rather should be tried as far as possible to see through the fundamental principles of data technology. This is valid for all youngsters, also for those in vocational training.
After all the mere habituation to the behavior of a "black box" is unworthy and will have consequences as far to production. ... Up to commercial and administrative education the principles of computer technology must be taught, as only by that way the occuring courses of events can be seen through and sources of errors can be detected. Thus may arise the possibility of an independent judgment". - So far Ernst Schuberth.
The second author deals with mathematical instruction in common, as by this time computers were still not present in schools. It is
Walther Lietzmann: Die Methodik des mathematischen Unterrichts (Methodology of Mathematical Instruction), Quelle & Meyer Heidelberg 1951, p. 9:
"The development of the opinions on the goals of calculating instruction is reflected by its history. Until 17th century it nearly totally emphasized practical purposes. The pupil was instructed how to do:
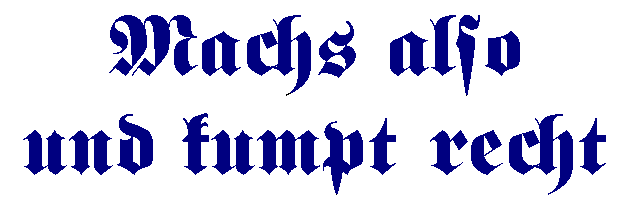 "Machs also - und kumpt recht" (Do it this way - and will come right) the Bamberg Rechenbuch of 1483 tells. Why this way should be gone stayed unanswered. So calculating was a handicraft, taught and learned as all the others. Teaching was dressing, instructing was swotting rules. Such a unilateral emphasis of the material principle has occasionally persisted into the 19th century.
"Machs also - und kumpt recht" (Do it this way - and will come right) the Bamberg Rechenbuch of 1483 tells. Why this way should be gone stayed unanswered. So calculating was a handicraft, taught and learned as all the others. Teaching was dressing, instructing was swotting rules. Such a unilateral emphasis of the material principle has occasionally persisted into the 19th century.
We may say - or at least hope - that nowadays this kind of calculating instruction has died out. The reversal began in the 18th century, decisive by the working of Pestalozzi. There was the new intention to form intelligence by calculating. Insight to the system of mathematical rules is not less important than knowledge and skill in execution. Thus the development of visual and logical qualifications became the main duty of mathematical education. Not rarely this formal principle was exaggerated, to teach more about the principles than to train the student's ability to use them properly. Gradually by time came an even balance between the formal and the material principle. Harnisch, Diesterweg and Hentschel should be mentioned."
This text of Walther Lietzmann can be transferred without any change to the situation of teaching informatics (and other technologies). By a more intense knowledge you may adhere to the opinion that things here went just the opposite way: By the beginning of computer instruction in the seventies and early eighties, the years following the introduction of "Modern Math" into the classrooms, teaching themes were: "What does a computer consist of?" - "How is it to be programmed (BASIC or Logo) to solve a problem?, a mainly formal principle. The reversal came by introducing PCs and Macintoshs into the classrooms. By the motto "is here anyone who understands this box?" and "a Macintosh - unable to open!" and with the improved facilities of readymade programs came the sight of the computer as a mere tool to enhance the mind and concentrate on what to do and how by using it. Until the intention to install it as a preferred teaching and learning aid, supporting or even replacing blackboard, projector, experimental assembly, and 'in the as we hope, not too distant future' as some progressive pedagogues wish, a replacement of school books and notes. Especially the multimedia technique is assumed to bear immense possibilities as well as the use of internet. Commonly quoted: "A today's motorist needs no knowledge of the engine."
"Machs also - und kumpt recht". Are we -five centuries ago- located back near the Bamberg book of calculating? The reason shines up evidently: It seems to be incredible difficult to immerge into a deeper knowledge of computer technology. And the adapted still superficial knowledge becomes obsolete in a shorter time than it took to achieve it! You may resign and I think the reduction on mere application is a result of this resignation.
B. Demands to a modern technological instruction
B 1. The dilemma of modern techniques: Easy to achieve, difficult to understand
An example from a neighbored place, common to us: the thermometer. Familiar to us, that 'real' thermometer invented by Galilei and Torricelli 400 years ago, many times improved, but unaltered by his function. Easy to understand: all blows up by heat, different by its kind. Experiments on that can easily performed at the home table, not only in the physics classroom. Even the reason can be understood if we imagine (and partly can observe) the fact of the restless thermal movement of the smallest parts of material.
There stay questions: how does the thermometer that is used, when I'm sick hold its temperature? How does the min-max-thermometer present to me its extreme showings at day and night? An elder person can explain it: I see!
When I was young I wondered about those bimetal-thermometers (with the needle in front, and when you open it, a spiral behind. How does it do? I needed a book as you cannot see the tricky structure of the spiral. But observed, touched, cautiously moved - I see!
And today? Digital thermometers with minimum and maximum, two sensors for inside and outside, showing tenths of a degree, a switch can choose centigrades or Fahrenheit and for a cheap money you can obtain them in a junk store! Do you know how they work? Opened them and inspected?? Touched, understood???

A Digital Thermometer inside - insight?
But how do they work? Pupils may ask you, perhaps only to bamboozle you as they can be sure of your ignorance... and - if you thanks to your special knowledge know it - what will you say?
B 2. The reality: Instruction oriented to using
You better refuse to give evidence! Either your correct explanation will be long lasting boring to your listeners or you can make a scrap statement using the words: constant current source, thermal dependent resistor, analog-digital converter, nematic liquid crystals, elliptic polarized light... Shut up!! Maybe it's right, but useless.
So you say: "Leave that aside. Now we take this thermometer to get the temperature of our experiment the most convenient way - or would you prefer that 'old' mercury thermometer?" That is the 'pragmatic' answer. This is called as "oriented to practice". That is a statement similar to "In a driving school of today there's no explanation of the carburettor." And why should they explain it? A modern car has none. May be there is an electronically controlled injection pump and if that does not work to drive the motor right away it is replaced - and that's that! It's cheaper than searching for the defect and repair it, says the mechanic anyway ond probably he will complain about the lousy firm delivering such a mess. You pay him, take your car and drive away and probably you will complain about that lousy mechanic unable to repair that intrusion automatic (or how did he say?)
Everywhere and at any time we are using things being happy, when we had understood the instructions to use it and we are very proud if we can teach that to others. The way of working inside? Mysterious... - No time, not interesting, no mystery as long as it works! And if it does not work anymore? We will buy a new one, a better one, the old one became oldfashioned anyway.
Do we have to be content with this attitude towards modern technology?
should we give this attitude to our pupils?
By a good conscience?
Or resignating?
B 3. The aim: Instruction to benefit the user.
The following refers to a German speciality: The German word for "Instruction to the user" is not only "Gebrauchsanweisung" but very often it is named "Bedienungsanleitung" (Instruction to serve) and it is common to say "eine Maschine bedienen" (serve a machine). I really hate this way of speech which involves a special way of humble thinking about machines...
I want to make users of technological products critical and self-confident to see the word "Computerbedienung" not as to serve the machine but the machine serving its user!
We shall dominate equipment not be its slave!
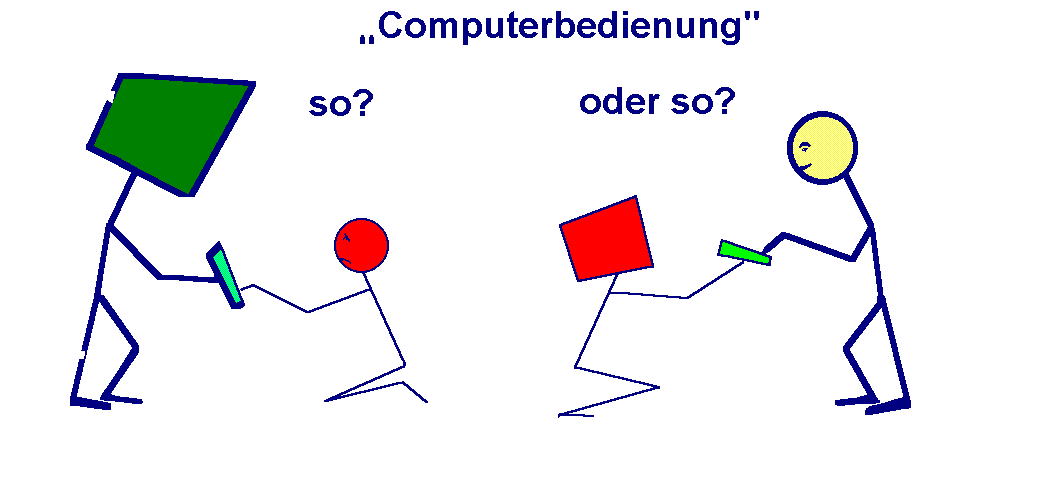
This picture arose by a course of informatics.
But asked confidentially: How should a human being learn that stuff, at 5 millions of transistors on a single chip, a Handbook for a programming language with 8000 pages advertised by shouting "Only 49 Deutschmark per Kilo!!". Obviously waste of time to swot that, even the attempt is punishable!
There remains the possibility to concentrate on the utmost essential. But what is it, the utmost essential? Here is a large space for private opinions and I see the following as my private way - would you follow me a part of it?
C. A Way to an adequate insight to the computer
An answer, before you have put the question: Teaching aids and texts as helping hands or walking sticks by the way I will sketch now, are not on sale. Help yourself...
C 1. Mechanical Calculators
At the beginning handle a mechanical counting device from an old electric meter or a speedometer. Playing with it and exploring it will occur by itself. Amazing this change from nine to ten and viceversa. You see the principle, understand it and perhaps you get an idea to build some of that kind. We leave it and look further, see the old mechanical helpers of times ago with understanding and respect - No, not the slide ruler, its sophisticated design leads us away from our way. We want to go the path of "digital"-counting calculating. But Abacus too is neglected, its principle is to memorize numbers, not to calculate with them, it is nearer to our use of pencil and paper when we are calculating in writing.
As farewell to the conceptual we take the fingers of our hands. The rash answer to the reason of our decimal system becomes a question when we realize that we with our two hands in a system based on six we easily could count unto 35: One hand shows from one to five, and the other will show each completed sixpack. In our decimal system we have to gesticulate by the Italien way: "Tr-en-ta cinque!"
Oh, if we all would have the dexterity of a well-trained pianist, in a dual system we could count and show numbers as different figures up to 1023...!
Dual system? - "Why, that's the way computers calculate!"
C 2. The Dual System - what's behind?
Dual counting
In classes I have realized: It is better if the students are not so much acquainted to the binary system now. They rather play with it and do not yet bear it as a mathematical overload. Then they will see early a rhythm by one, two, four and so on, the "stubbornness" of the system developing.
Table of Numbers written binary
| 0 | 00000
|
| 1 | 00001
|
| 2 | 00010
|
| 3 | 00011
|
| 4 | 00100
|
| 5 | 00101
|
| 6 | 00110
|
| 7 | 00111
|
| 8 | 01000
|
| 9 | 01001
|
| 10 | 01010
|
| 11 | 01011
|
| 12 | 01100
|
| 13 | 01101
|
| 14 | 01110
|
| 15 | 01111
|
| 16 | 10000
|
| 17 | 10001
|
and so on...
|
Dual addition and multiplication
But relations to arithmetics is to be built: The pupils must see how simple (and familiar) binary addition is. One plus one is still two. Only the two is written in a different way! And how enviably simple is multiplication! It goes the "Hamlet way": To write and add or not to write and not to add, that's the question... Most simple is the "multiplication table": One by One is One, all else is nought. Essential are comparisons with decimal calculations to show the binary way to be allright. Here I leave away subtraction and division, that is too sophisticated now.
I rather tell of Leibniz, who had dealt with the binary system and by this occasion discovered the system of antique chineses number signs
Dual thinking
Now a hint is to be made, that we generally like to think in a 'dual' way:
| left
| -
| right
|
| clair
| -
| dark
|
| up
| -
| down
|
| friend
| -
| enemy
|
| good
| -
| evil
|
| God
| -
| Devil
|
are such couples of terms, expandable as you like. Tertium non datur, there is no third between, The middle becomes a borderline between two alternatives. There is no need to think that way in life but in this place this schematic pattern is to be cultivated, we will use it.
Logical: If - Then
Another common pattern: All has a reason, exaggerated: Somebody has to be found as guilty for happening this or that. We stay calm and say: If - then.
If it is raining or snowing and I open my umbrella and the umbrella has no hole then I will not become wettened. You may construct contraries and combine them and look for correctness - it is a nice playground.
And by the way we learn about the combination of conditions and results - about and, or, not and learn to write them with capitals when we give them a 'logical' meaning: AND, OR, NOT
Two other examples:
- If you talk OR she speaks, then I hear you.
- If you talk OR she speaks, then I understand you - but NOT when you both are speaking.
This is an either - or. we will meet it in the future sometimes - and in a variety of disguise! Its official name: EXCLUSIVE OR (XOR)
Two switches and two lights ...
After we took some time and concentration on this aspect I hand this box out to the pupils:

After some switching about it turns out:
1. To light the green lamp on the left side, both switches must be in the "down" position
2. To light the red lamp, one switch has to be "up" (no matter which one), the other must be "down". You may also see the two switches in different positions or say: they must not be equal
3. You cannot light both lamps at once.
And by using our new technical knowledge we can express it this way:
- If the left AND the right switch are down then the green Lamp will be on.
- If either the left or (XOR) the right switch is down, then the red Lamp will be on.
I can put that into a table with all four possible switch positions:
| Left switch
| Right switch
| Green lamp
| Red lamp
|
| up
| up
| off
| off
|
| up
| down
| off
| ON
|
| down
| up
| off
| ON
|
| down
| down
| ON
| off
|
|
| Function:
| AND
| EXCLUSIVE OR
|
You may open the box and have a look inside and get an insight why the box works this way.

You may remind that such combinations of switches can be found in the household, the one at the ends of a longer corridor, the other by fuse and lamp switch.
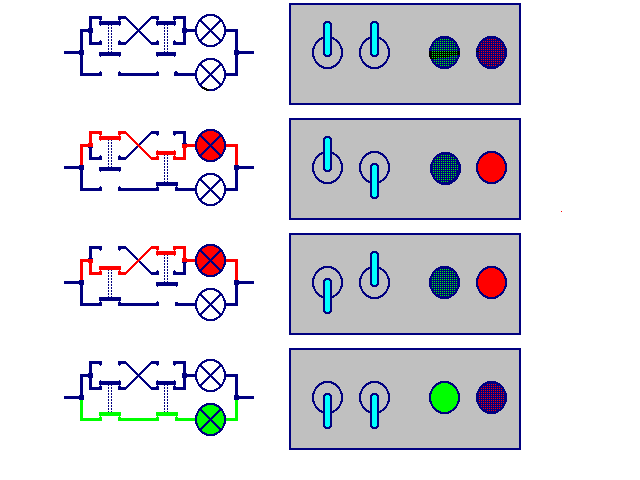
we replace the words "up" and "down" as well as "on" and "off" by two abstract symbols e.g. dash and circle. Then the table becomes more handsome, especially when we replace the names of the switches and of the lamps by the letters A, B, D and E:
| A
| B
| D
| E
|
| O
| O
| O
| O
|
| O
| I
| O
| I
|
| I
| O
| O
| I
|
| I
| I
| I
| O
|
(The intention is evident: Circle and dash are similar to 0 and 1, but the way of writing does not matter. Necessary is only: it must be two different, well distinguishable signs)
... a calculator?

And suddenly the picture turns down like this double-sensed grafic by E. Borer, you may see:
| A
| +
| B
| =
| D
| E
|
| O
| +
| O
| =
| O
| O
| Zero... |
| O
| +
| I
| =
| O
| I
| One... |
| I
| +
| O
| =
| O
| I
| One...
|
| I
| +
| I
| =
| I
| O
| Two!
|
The box shows us in a binary way how many switches are in a down position!
That thing can count up to two!
Really? Can it add?
No, not at all! We have found in this lawful, but senseless lighting of the lamps our learned calculating. We can intend a purpose, we could blame it for doing what we intend to do. It does like we want, but it does as if...
If we could not calculate, the box won't be able either!
It is indispensable to get clear about this fact.
Many pupils adhere to the idea, the right solutions of every problem would be stored in the calculator - it "knows it" or at least "it can". Smarties would say "It's a chip. That can do it!"
I can reduce the addition of two binary numbers merely to an If-Then - decision without any mathematical knowledge and in the case of an electronic calculator it is electric: If line one has voltage (the pupils may say: "juice") and line 2 has voltage then make...
- Calculating is done by the user!
- Even then, when a key is pressed with a pattern looking similar to "1".
- A user who has never learned the patterns and who knows nothing about calculating cannot be assisted by a most expensive pocket calculator!
- It is really important to make students conscious how intelligent they still are when they believe to be unable to calculate without that "handsoap". It might encourage them to try it occasionally without it!
- Therefore this explanation is essential: The working out of the pressed keys and the presentation of the results by the display are in all cases merely If-Then - decisions.
- But looking for the right keys, recognizing the showings of the display and - thinking about the possibility of the correctness of the result - that is our own achievement, that is the actual calculating,
But how noW - that box is unable to count until three... How should a table look to achieve that?
Thre switches are to be used and still two lamps...
| Left switch
| Middle switch
| right switch
| green lamp
| red lamp
|
| A
| +
| B
| +
| C
| =
| D
| E
| and we
think
|
| up
| up
| up
| off
| off
|
| V
| +
| O
| +
| O
| =
| O
| O
| "zero"
|
| up
| up
| down
| off
| ON
|
| O
| +
| O
| +
| I
| =
| O
| I
| "one"
|
| up
| down
| up
| off
| ON
|
| O
| +
| I
| +
| O
| =
| O
| I
| "one"
|
| down
| up
| up
| off
| ON
|
| I
| +
| O
| +
| O
| =
| O
| I
| "one"
|
| up
| down
| down
| ON
| off
|
| O
| +
| I
| +
| 1
| =
| I
| O
| "two"
|
| down
| up
| down
| ON
| off
|
| I
| +
| O
| +
| I
| =
| I
| O
| "two"
|
| down
| down
| up
| ON
| off
|
| I
| +
| I
| +
| O
| =
| I
| O
| "two"
|
| down
| down
| down
| ON
| ON
|
| I
| +
| I
| +
| I
| =
| I
| I
| "three"
|
And how should it been shaped to achieve that?
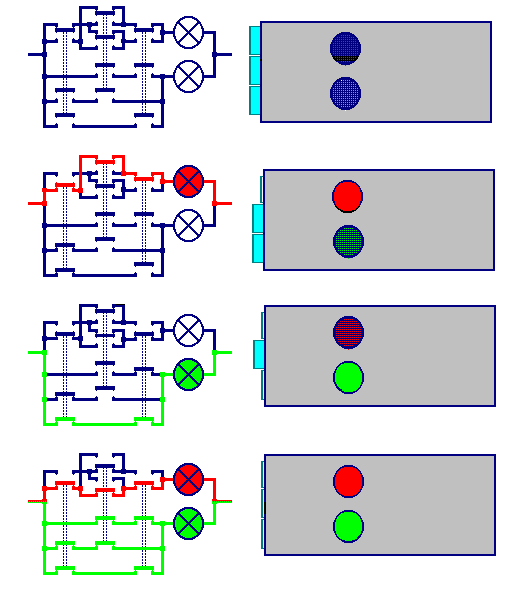
Oh no, that looks rather complicated and it cannot be done with normal toggle switches. You would need packed switches. he mechanics becomes confusing. As we want to explain the workinkg of a computer to all but do not want to raise technicians, We should leave here. A transition is to b made, in practice and by description.
Transition to Electronic Parts
In practice we leave the toggle switches actuated by human fingers and will use miniaturized switches driven by electricity. An electromagnetically actuated relay switch may be our intermediate server as it had been in computer history with Zuse and Aiken more than half a century ago.
Today transistors are used.
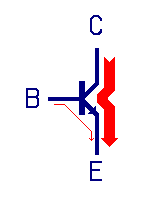 But I cut out the explanation of a transistor switch. I present its possibility to conduct from C to E if there is a tiny opening current from B to E. I show it under the microscope, showing that there is really nothing to observe:
But I cut out the explanation of a transistor switch. I present its possibility to conduct from C to E if there is a tiny opening current from B to E. I show it under the microscope, showing that there is really nothing to observe:

Here I actually use a "black box" as normal kids never would comprehend the function of a p-n-transition.
As we will scarcely educate former semiconductor producers I may put the declaration:
It is a complete nonsense and waste of time to fill the kids' brains with useless stuff they never can understand!
As we combine two toggle switches to an array we can give a 'logical name' we can do the same with transistors. Such arrays are named as "gate". Their construction is deciding under which conditions of the normally two "input" contacts the normally single output will have a low or high potential, which can be conducted to further gates (or e.g. lamps to show a result).
It is the same situation as with the lamp boxes we just have used. Their behavior is strictly dependent on their inner construction and the position of the input switches. Actually important is the possibility of miniaturizing to "Integrated circuits" That can roughly been shown by the production of a printed board in a practical training which may give an outlook to sub-miniaturized mass production by huge enterprizes.
Transition to the Gate Symbol
Not only in practice but in description too a transition should be made: The transition from the array of switches to the gate symbol.
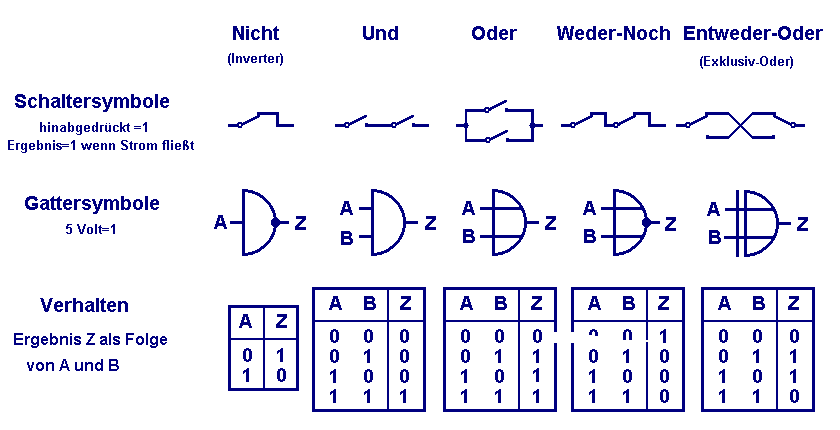
No longer represents its drawing the way of action (as the switch symbol still did similar to an Egyptian hieroglyph). It is an empty sleeve getting its contents and meaning only by definition, similar to the fact that our Latin letters give no hint how to spell them. Five important types are presented here, a speciality is the inverter, always giving as result the opposite of its (single) input.
The gate symbol gives us only evidence of what it does, nothing about how it is done.
But we have seen how it could be done
And we have seen (by the adder) how important a sight from several sides on the same object can be!
By the way, we can see the adder (not necessarily!) as a combination of AND and XOR...
 Here we need a solid stock of experimental material, otherwise the stuff will become a dry dusty desert. And the area has to be clearly furthermore. But it is a good way to play with the inverters, the ANDs the ORs the XORs and their inversions.
Here we need a solid stock of experimental material, otherwise the stuff will become a dry dusty desert. And the area has to be clearly furthermore. But it is a good way to play with the inverters, the ANDs the ORs the XORs and their inversions.
It is now time for the question how many different types of gates with two inputs and one output might be possible...
The logical answer to it will puzzle even the discoverer! And after that the astonishing feat that each of these 16 functions can be achieved by combining e.g. OR-gates and inverters:
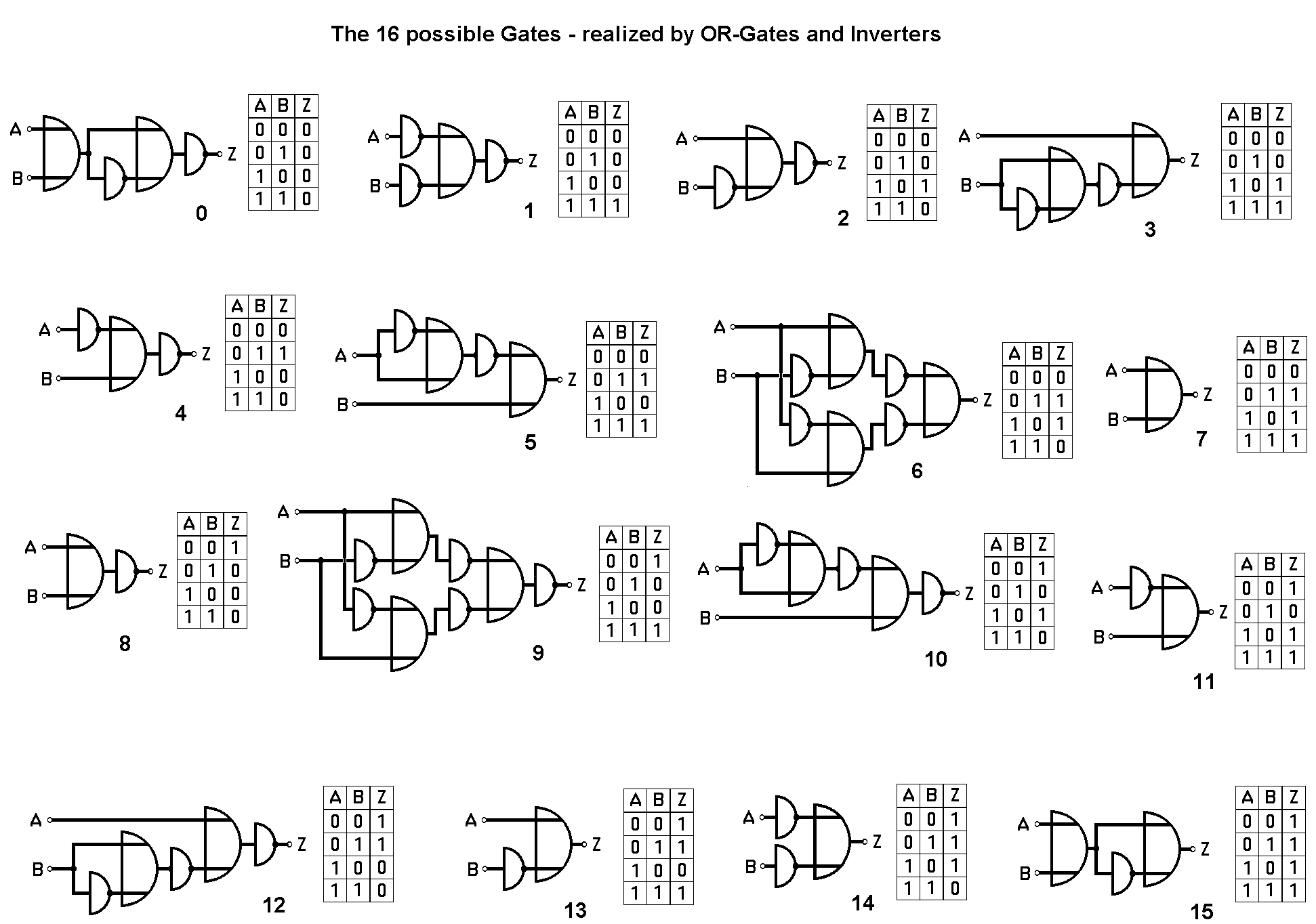
Combined Logics
As if I invert an OR afterwards, it will be a NOR. And if I invert the signals before the OR, will it be the same? A common situation at educating a child: "When you talk or make a mess during supper, you will get no pudding afterwards and go to bed immediately."
"If you don't talk or don't make a mess..." then the until now silent, totally stained but clever child will cry: "I want my pudding! I had not said any word yet!" Make it better next time by saying "If you don't talk and don't make a mess..." You see: If NOT A AND NOT B Then is the same as IF A OR B Then NOT - even neither A NOR B.
C 3. A matter of view - Either-or - or what?
And once more back to either-or or exclusive or.
How did it do and where was it useful?
- If A OR B is "1" (but not both), the Z is "1".
So it was used to get the sum of two binary numbers, as odd numbers have the end 1, even numbers end by 0. And when I add two odd numbers the result will be even, adding an even number to an odd number will result in an odd number.
- I can say: If A und B are equal, then is Z = 0. So I can use ist as test for equality.
- But I may also say: If A = 0 Then is Z = B and If A = 1 Then is Z the inversion of B.
B is inverted, if A = 1.
Now my XOR became a controllable Inverter for B able to leave the signal B unchanged by the condition on A
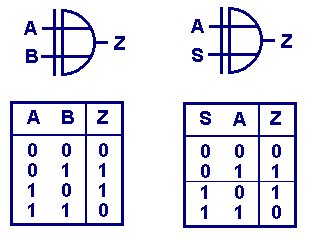
Important now: I have not invented a new building block merely I used a well-known fact by looking from an other side for a new purpose:
Such controllable Inverters, (XOR-Gates) around a "normal" Gate, an OR-GATE for example:
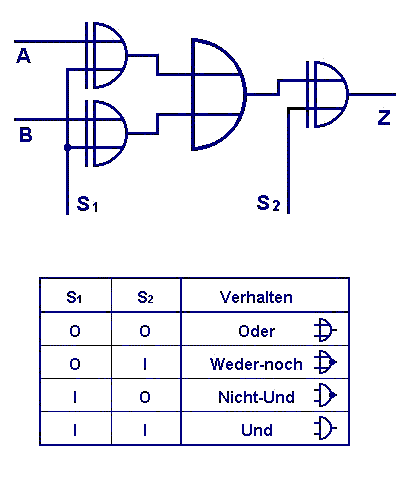 This group lost its constructed stiffness - we got a "Universal Gate" to whom we can give control signals, how it should manage the data signals: OR / NOR / NOT AND (NAND) / AND.
This group lost its constructed stiffness - we got a "Universal Gate" to whom we can give control signals, how it should manage the data signals: OR / NOR / NOT AND (NAND) / AND.
C 4. Mikroprocessor - I see!
Here the door opens to umderstand a computer as universal machine. The principle of the controlled inverter is the basis of the microprocessor. Therefore I can make the same computer do very different things by loading just the adequate program without a need to change anything by its construction.
D. Outlook and end
I had asked you to follow me on a part of my way to understand the computer. I hope you have not the feeling to have been on a wrong way all the time. You may have noticed what you need on that walk to get a benefit of it: Enjoy thinking round the corner! Look at the other side of things to get a never guessed imperssion and perspective. The example of the XOR-Gate showed that "exemplarily" and I think we should cultivate this kind of positive-critical thinking.
We stay here and look out: The possibility to combine these gates to memories and counters, decoders to show us the results in a common way. Processors and surroundings are combined to the computer, Stored control data are combined to programs. -
Now we go back: Processor, Universal gate, controlled Inverter - that was the 'exclusive or' found in the adder pretending to be a counter as well as in the corridor light-switch... We pass that old woman, that witch we could ask "What is reality now? But facing her what she would say the young lady turns away and gives no answer.
Further back to the calculating machines
The Abacus I left aside looks at me a little sneering: "At the beginning of your lesson you said that my purpose is merely memorizing, like paper and pencil. Do you think a computer is much better? Real thinking is your job anyway!" He may be right, this old sage from far east...
And now we have reached the rumorous Data Highway, sit by our computer and start. More thoughtful?
-------------------------------------------------------
This text is mainly going along a lecture I held in Hildesheim University on November 6, 1996 by the occasion of the Wagenschein Centennial. It is published in "Der Vorrang des Verstehens - Beiträge zur Pädagogik Martin Wagenscheins" (Klinkhardt)
[1] Technical progress is marching on: In 2001 -only five years later- the operating system (!) Windows XP consists of a billion of instructions, processors are constructed with several hundreds of millions of transistors - a nearly exponential growth... but the principle has not changed since the 1950s.
[Back into text]